|
On parle aussi de "théorie de la forme" en français. Cette théorie allemande est une théorie psychologique de la perception. Le débat sur les origines de cette théorie nous mèneraient trop loin, nous ne l'aborderons pas. Sachez cependant qu'avant d'être appliquée au graphisme, cette théorie est avant tout un mouvement scientifique qui s'oppose à d'autres mouvements qui n'ont rien à voir avec le graphisme.
Je connais cet aspect car il est célèbre dans les domaines du graphisme, puisqu'il était approfondi dans l'illustre école du Bauhaus (ancêtre du design), avant que celle-ci ne soit fermée à la 2nde guerre par les Allemands. C'est probablement la seule "théorie" que je connaisse qui fasse à ce point le lien entre les science et les arts graphiques. Et à bien creuser, on s'aperçoit que cette "Gestalt" nous raconte beaucoup de choses sur les pixels.
Sur le sujet qui nous intéresse, la Gestalt a établi des principes généraux définissant notre perception au sens large, et donc aussi, au niveau visuel. Son principe général est qu'on perçoit avant tout l'ensemble, indépendamment de la structure qui le compose. Si cela semble évident sous cet angle, cette Gestalt a le mérite de formaliser des éléments clé sur ce qu'on a tous les jours sous les yeux, permettant ainsi de le traiter autrement, par la maîtrise de ces points de grammaire visuels.
Je suis tenté de faire une analogie avec une autre période des arts qui exploitait certains éléments que l'on pourrait retrouver dans cette Gestalt : les lignes de force. Cet aspect est beaucoup plus connu des graphistes et régit la formalisation d'une mise en page, d'une sculpture, d'un cadrage ou de n'importe quelle composition. Ce sont des lignes visuellement "fortes" qui orientent le regard d'un côté à l'autre d'une chose observée. Cela peut être un lien visuel d'un objet à l'autre, d'une statue à l'autre, un élément de perspective orientant le regard. On arrive même ici à une corrélation avec les règles d'harmonie. Pour mieux être compris des programmeurs, je parlerais de "macro éléments graphiques" pouvant être composés d'autres éléments plus petits. Des chercheurs ont découvert que cette image était perçue "avant" les détails et permettait d'avoir une interprétation de l'image avant de comprendre la chose vue : c'est par exemple ce qui permet d'éviter un danger qui arrive avant de l'identifier (une boule de papier que vous voyez arriver au dernier moment et déclenchera un réflexe démesuré).
La Gestalt se situe donc à un niveau beaucoup plus fondamental sur la perception des choses, et sur la vision pour le sujet qui nous intéresse. Elle nous apportera des solutions essentiellement sur le dessin de l'infiniment petit.
1- Théorie graphique
1.1- Le tout est différent de la somme de ses parties
Les éléments que l'on regarde sont indissociables de l'ensemble qu'ils composent. Par exemple, lorsque vous regardez un carré, il ne sera compréhensible que si vous considérez l'ensemble des éléments qui le composent. Aussi il est par exemple possible de représenter un triangle sans pour autant qu'il existe formellement.
 |
| Cette figure de Kanista montre un triangle qui n'existe pas formellement dans l'image. On le voit parce qu'on cherche à le voir. |
1.2- Notion de "contexte graphique"
Le simple fait d'avoir à considérer par exemple que le contexte est "un objet éclairé sur fond sombre" ou le contraire amène à interpréter une image différemment. Certaines images très connues défilent ainsi sur des séminaires de communication pour montrer que l'approche d'un spectateur modifie sa compréhension du sujet observé. Un observateur aura par exemple besoin d'un contexte pour comprendre l'orientation d'un cube filaire en vue isométrique : est-ce qu'il tourne vers la droite ou vers la gauche, etc.
 |
|
 |
| Le vase de rubin est célèbre pour montrer qu'on voit ce que nous sommes disposés à voir : la forme claire ou la forme sombre. |
|
Cette "forme ambigüe" vieille d'un siècle tourne aujourd'hui dans tous les séminaires de communication. Certains voient en premier une jeune femme, les autres voient la vieille femme. |
Je me permets au passage de faire un peu de publicité à mon propre site de photographies abstraites, où le spectateur perd totalement le contexte de ce qui est photographié et perd en même temps tout repère. Il a souvent tendance à "chercher à y voir quelque chose", ce qui est finalement assez curieux. On rejoint ici de principe de la Gestalt, où le spectateur cherche une forme singulière pour interpréter ce qu'il voit.
 |
|
 |
| Tout le monde le sait : l'avenir est écrit dans le marc de café... ce marc qui prend les formes les plus fantaisistes en se déposant, nous permet d'y voir... tout ce qu'on aimerait y voir ! La Gestalt, c'est l'avenir ! (photo : Thierry) |
|
Dans ce genre d'image, comme lorsque l'on voit des nuages, on est tenté de trouver des formes, de chercher quelque chose de familier. J'ai eu de nombreux témoignages de gens voyant dans cette image des choses très variées. (photo : moi) |
1.3- Recherche de cohérence entre les formes / points.
C'est ici le point le plus important de cette théorie, si on considère notre approche par le pixel. En effet, les pixels posant une limite nette entre ce qu'il est possible ou non de dessiner, cette théorie permet d'étendre la réflexion à ce qu'il est possible de représenter, au-delà du dessin.
L'exemple le plus basique sera par exemple de dessiner 3 pixels equidistants. N'importe qui sera capable d'y voir un triangle. Pourtant ce triangle ne sera pas dessiné. Il sera une interprétation cohérente, permettant d'appréhender ces 3 pixels comme un tout. Les implications par rapport aux contraintes des pixels sont d'ailleurs nombreuses. Cela amènera l'œil à considérer comme une ligne droite les pixels étant sur une même ligne, même si elle est discontinue. L'idée est de supprimer un artéfact là où le dessin n'est pas utile.
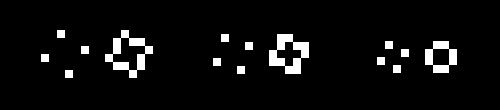 |
| Ci-dessus, 3 carrés différents en taille et en angle, représentés uniquement par les 4 pixels de leurs angles. À droite de ces carrés, les sommets sont reliés par leurs arrêtes. On voit nettement que les artéfacts ne permettent même plus d'identifier précisément les formes. |
1.4- Lois d'organisation perceptive.
Cette théorie a figé certaines lois élémentaires décrivant la façon que l'on a de percevoir les choses (les voir en ce qui nous concerne) :
|
Proximité :
Nous réunissons ce qui est proche dans l'espace. La proximité des éléments nous amène à les croire appartenir à un même tout.
|
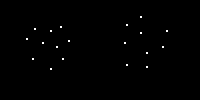 |
|
Continuité :
Nous cherchons un cheminement entre les points que nous voyons. C'est typiquement ce qui nous permet de comprendre les images en dots 3D par exemple.
|
 |
|
Similarité :
Nous regroupons ce qui se ressemble (qui se ressemble s'assemble).
|
 |
|
Fermeture :
Nous cherchons à fermer les formes qui ne sont pas complètes. Comme si l'esprit avait besoin de fermer les portes !
|
 |
|
Familiarité :
On cherche les "bonnes formes", ce sont des formes qui nous sont familières : on cherche une ressemblance entre ce qu'on voit et ce qui nous est connu.
|
 |
|
Destin commun :
Lorsque des points bougent, on regroupera en une unité les points ayant le même déplacement. On cherchera une cohésion de mouvement.
|
 |
2- Applications sur les pixels
2.1- Deux points suffisent à définir une droite
C'est vrai en maths, mais c'est un peu vrai aussi en graphisme : il suffit de 2 points pour tracer une droite. Naturellement, sur un écran d'ordinateur, la droite ainsi définie sera assez vide. Ce sera presque "l'idée d'une droite". Mais naturellement, cette règle ne vaut que si vous n'avez rien d'autre à l'écran. Car il suffirait d'un 3ème point pour dévier la droite d'origine en 2 segments de droite joints par le point central par exemple.
 |
| Ci-dessus, 2 points que l'imaginaire relie en une droite.
|
 |
| Ci-dessus, ces 2 même points sont séparés par 2 autres points. Alors on ne voit plus la droite d'origine, mais 3 segments formant un chemin. |
Cette règle a cependant un vraie vérité vraie : lorsque vous devez à tout prix dessiner une forme simple (ou géométrique), le mieux est parfois de s'abstenir de dessiner tous les pixels de ladite forme. En laissant une part de travail à l'esprit qui regarde l'image, on peut parfois gagner en résolution. Par exemple, lorsqu'une demo affiche des formes 3D sous forme de points (ou 3D dots), on ne ressent pas cette notion de "facettes" qui existerait si tous ces points étaient liés par des segments. C'est d'autant plus vrai que la résolution est basse, et donc les artéfacts importants !
Mais rendre une forme discontinue pose toutefois un problème : cette forme intervenant dans un contexte (une image, une couleur, un motif), ce motif risque d'interférer, voire prendre le pas sur notre forme discontinue. Le principe consiste alors donc à laisser la forme "floue", quitte à abuser d'antialiasing, là où la forme n'est pas absolument dessinable, et au contraire de bien marquer les pixels clé qui permettront de bien définir la forme à représenter.
 
Pour cette image de la Rebellion, Ced et Barjack ont eu besoin de dessiner
des lignes qui étaient "entre" les pixels. Ils ont dont créé une zone floue,
et les yeux pallient eux-même pour compenser l'absence de détail.
2.2- Tracer une courbe
La problématique est absolument la même que pour une droite, au détail près que la courbe est une forme plus complexe que la droite, et donc identifiable visuellement de façon moins "évidente" par l'observateur. Une courbe peut représenter une perspective complexe, ou un élément vu de face avec cette forme par exemple. Il conviendra donc bien de marquer le relief par le choix des couleurs utilisées. Il faut aussi bien comprendre qu'une courbe nécessite d'afficher davantage de points pour être représentée. La technique ci-dessus reste vraie, mais plus délicate à exploiter. C'est le principe de continuité qui nous sera utile.
2.3- Masquer les artéfacts d'une courbe
Lorsque vous dessinez certaines formes, compte tenu du manque de précision des pixels (dû à leur taille ou à leur position), certains pixels semblent "déborder" de la forme prévue. La Gestalttheorie nous apprend précisément que ces artéfacts étant hors de la forme que l'on souhaite représenter, risquent de ressortir particulièrement. En fait, ces points risquent de devenir visuellement importants alors qu'ils devraient être anodins. Nous avons vu comment la technique du hinting permet de réduire dans une certaine mesure ce problème, l'antialiasing aussi. Mais ces techniques visant à lisser une forme peuvent aussi être complétées par d'autres astuces : on peut par exemple faire passer une autre forme à l'endroit de l'artéfact, le faisant utilement participer à la forme de l'objet. On peut aussi noyer ce défaut dans un "grain" de l'image. Par exemple, si l'image est riche en trames, il sera possible de masquer ce défaut en utilisant des trames à cet endroit précis. Une autre astuce consiste à détourner l'attention. Si ce pixel un peu trop saillant gêne l'attention, alors on pourra penser à faire apparaître un autre point lumineux ou coloré à proximité du défaut, le rendant proportionnellement insignifiant.
2.4- Isoler un détail en le détourant
Dans une image très chargée en éléments graphiques, il est parfois difficile de faire ressortir un détail, ou tout simplement, de ne pas confondre ces pixels avec le reste de l'image, leur conserver un contexte propre. Il est important que le nez de tel personnage (par exemple) ne faisant que 2 pixels de large ne soit pas pris pour un pli du rideau qui est en arrière-plan. La tehnique est très simple : il suffit de détourer l'objet. Ce genre de détourage est généralement noir ou assombri à défaut. Cela nous ramène à la propriété de la couleur sombre de sembler plus lointaine, et donc l'objet qui s'y trouve représenté en clarté ressort en avant, détaché de son environnement.
3- Exemples concrets
3.1- Un pixel peut changer la forme qu'il ne dessine pas
En changeant l'allure générale d'un dessin, un simple pixel peut donner à voir une forme différente à un contour qu'il ne dessine pas. Ci-dessous un exemple sur un mini dessin. Pour grossir l'effet, j'ai séparé les 2 versions histoire de minimiser l'influence de l'un sur l'autre.
 |
Cet exemple a besoin d'une certaine distance avec l'écran pour mieux fonctionner.
Les 2 images de gauche et de droite n'ont qu'un pixel de différence. L'image de gauche nous donne à imaginer un trèfle à 4 feuilles ou une croix allemande penchée à 45°.
Il suffit de lui retirer le pixel central pour redonner clairement une forme de dièse à cette image.
|
 |
Autre exemple : la taille du cercle noir ci-dessous semble légèrement différente selon que le tracé blanc semble suivre le cercle ou représenter un carré. Dans un cas, on assimile la taille du cercle noir à celui du cercle blanc (sans réllement intégrer son épaisseur), dans l'autre, on "étrique" le cercle noir dans un carré de la taille du cercle.
3.2- Forcer les formes élémentaires
Les formes élémentaires sont des éléments graphiques incontournables (que ce soit pour des raisons culturelles ou biologiques). Essayer de les mettre en valeur permet parfois de mieux cerner une forme.
 |
Cet exemple a besoin d'une certaine distance avec l'écran pour mieux fonctionner.
À gauche, l'image ressemble à une croix couchée (ce qu'elle est). À droite, en démarquant le triangle on renforce la compréhension d'une flèche.
|
 |
3.3- La force de la continuité
L'exemple ci-dessous vient du jeu "marche à l'ombre". Dans cette image on voit une image en seulement 2 couleurs, qui parvient malgré la richesse du jardin de l'arrière-plan (trames, bosquets) à dessiner une grille en premiers plan. Cette grille est lisible pour 2 raisons : la régularité de la maille la rend reconnaissable, mais surtout, chaque barre de la grille est prolongée en blanc, au niveau du ciel nocturne. La ligne a beau être discontinue au niveau de la couleur, c'est bien de sa forme qu'il s'agit.

3.4- Casser un motif pour suggérer un détail
Dans certains cas, plusieurs formes peuvent se battre en duel pour essayer de gagner l'une sur l'autre, aux dépens de ce que l'on souhaite montrer. Ce petit exemple montre une ligne agrémentée de "pics" représentés par des pixels dépassant de la ligne horizontale. La version de droite tente même de casser la ligne à l'endroit des pics pour suggérer le décrochement. Mais systématiquement, les pics ressemblent à des crénelages sur la ligne. Le seul moyen de suggérer ces dentures est de casser suffisemment la ligne pour que la forme élémentaire la plus marquante soit le triangle. Alors, les pics apparaissent enfin.
3.5- Conflit sur les trames.
Tous ceux qui ont un jour eu à dessiner sur une trame savent combien elle peut entrer en conflit avec la forme qui la recouvre. Le plus sûr moyen de sauver la forme en question, si elle est petite, est de la détourer, sachant que ce détourage subira aussi un conflit de forme avec la trame.
 |
Ci-contre, un petit disque de 7 pixels de diamètres sur les pixels paires (1ère ligne) ou impaires (2ème ligne) : le conflit donne un résultat différent. Différents détourages faisant apparaître des artéfacts différents, plus ou moins voyant. Le choix devra prendre en compte ces paramètres. |
 |
Une solution, lorsque c'est possible, est d'utiliser une 3ème voire 4ème couleur pour fondre l'artéfact dans le flou. Mais alors, l'intérêt de la trame ne serait pas de simuler une teinte (qui est dans la palette disponible), mais bien d'avoir une texture "tramée" à l'écran. |
 |
L'effet sera évidemment plus discret (voire tout à fait acceptable) si la couleur de trame est différente de celle du disque. Le meilleur résultat sera lorsque l'objet aura un contraste beaucoup plus marqué que celui de la trame. |
3.6- Éviter les motifs dans les dégradés
Sur les dégradés, les paliers de couleurs sont eux-même des éléments de dessin pouvant former des lignes. Il est parfois prudent de les casser pour éviter au dégradé de ne porter une texture trop prégnante.
 |
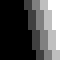 |
À gauche, un dégradé dont tous les paliers arrivent à la même hauteur. Le décalage de couleur se fait en dessinant des lignes horizontales. Vu de loin, il ressort de ce dégradé des lignes horizontales plus visibles que les paliers du dégradé. |
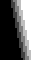 |
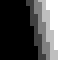 |
Ce 2ème exemple montre le même dégradé avec des paliers décalés d'une couleur à l'autre. Si cela fait apparaître une sorte de texture au dégradé, il adoucit en revanche les escaliers de la pente, en évitant de les propager et faire ressortir ces lignes horizontales. |
3.7- Dans l'infiniment petit, les formes sont toutes relatives...
Petit exemple pour montrer comment la somme de 2 carrés peut donner un cercle... ci-dessous, la somme (représentée au milieu) des 2 carrés (représentés à droite et à gauche) définit un cercle. Il devient même difficile de discerner les 2 formes élémentaires dans cette formes combinée.
|

