|
Il pourrait sembler naïf de vous parler du pixel tant ce qu'il est peut paraître évident à des gens déjà initiés au CPC. Je souhaite surtout ici vous donner un angle d'observation qui sera celui que je traite tout au long de mes articles sur le graphisme. Il y a la définition académique qui ne nous apprend pas grand chose, mais il y a surtout différentes approches possibles du pixel ; les enseignements que l'on peut en tirer est beaucoup plus riche.
Expédions rapidement la définition du pixel, qui vient de l'anglais "Picture Element", c'est la plus petite unité constituant une image échantillonnée. Il est donc indivisible. Le pixel a une taille donnée : la taille de "UN". "UN" quoi ? Un pixel, bien sûr !
Mais en fait, cette définition amène à se poser des questions sur la nature des pixels : peut-on les modifier ? Comment peut-on les afficher ? C'est pourquoi je propose dans cet article de définir non pas "LE" pixel, mais "TROIS" différentes définitions pour un pixel, selon son usage et ses contraintes, les différentes étapes de son existence. Les 3 définitions ci-dessous sont étayées au cours de cet article.
- Pixels enregistrés (en mémoire) :
C'est l'équation zéro d'une image : on définit une matrice de point qui vont définir l'image. Ces pixels n'ont pas de rendu réel, ils sont définis uniquement par des données enregistrées. Ils ne sont pas nécessairement numérisés, car chaque donnée peut être analogique. Il s'agit en fait simplement d'enregistrements bout à bout et permettant de décrire une image. À ce stade, le pixel n'est pas nécessairement encodé pour être affichable. Par contre, puisqu'il est enregistré, il est modifiable.
- Pixels encodés (pour / par le GPU) :
C'est l'image telle qu'elle existe au niveau électrique, dans un signal. Elle existe sous cette forme juste après avoir été créée par le contrôleur vidéo d'un ordinateur par exemple. Les pixels ont été lus par ce contrôleur (depuis une mémoire par exemple), puis interprétés de façon à transmettre un signal fidèle à ce qu'était capable de restituer l'ordinateur. Il affiche donc l'image en fonction de ses possibilités, avec les limitations qui lui sont liées, en terme de taille ou de limitations de couleurs. Ces pixels intègrent donc les contraintes techniques d'une machine.
- Pixels affichés (par un périphérique) :
Lorsque l'image existe sous forme d'un signal, elle est traduite par un périphérique, de façon à être vue par nos yeux. Cette image peut apparaître sur un écran ou sous la forme d'une impression par exemple. Le signal représentant un pixel sera alors traduit dans une forme très variable selon le medium (périphérique) utilisé.
Cycle de vie d'un pixel
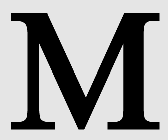 |
 |
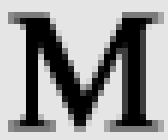 |
 |
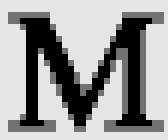 |
 |
 |
|
Source :
Avant d'être pixélisée, l'image source est parfaite.
|
|
Pixels enregistrés
Il ne sont pas nécessairement affichables en l'état par un CPC, ils peuvent être analogiques ou numériques.
|
|
Pixels encodés :
Les pixels sont affichables par le CPC, car adapté à ses contraintes techniques
(3 niveaux de gris).
|
|
Pixels affichés :
Le rendu des pixels est nettement différent. Les pixels subissent des contraintes d'affichage.
|
1- Pixels enregistrés (stockable en mémoire) :
C'est le plus petit point d'une image que l'utilisateur peut enregistrer.
1.1- L'échantillonnage :
La première étape avant la numérisation d'une image est l'échantillonnage. L'échantillonnage est une opération consistant à tronçonner un signal en petites parties dites unitaires. Ces tronçons ont généralement tous la même taille bien qu'il existe des cas où chaque échantillon a une taille différente. Chaque tronçon contient une infinité d'informations. Lorsqu'il s'agit d'échantillonner une musique, les tronçons peuvent être définis par leur durée (on parle souvent d'échantillons). Pour l'image, ces tronçons sont représentés par des dimensions de la taille de nos chers pixels (je simplifie un peu). Ces pixels contiennent donc une portion d'image.
Il convient ensuite de résumer le contenu de ce tronçon par une donnée unique. À cette étape, la valeur peut être infinie (analogique), pourvu qu'il n'y en ait qu'une par tronçon. Cette valeur pourra par exemple être une sorte de "moyenne" de ce qu'on a observé à l'intérieur du tronçon (on a le choix de la méthode). Par exemple, les capteurs CCD des appareils photo numérique stockent une tension analogique liée à la quantité de photons ayant impressionné la surface du pixel. On pourra aussi choisir un certain nombre de critères pour résumer ce pixel. On retient souvent la quantité de rouge, de vert et de bleu qui le composent. On pourrait plutôt choisir d'enregistrer la quantité de lumière sur une bande infrarouge par exemple, ou un échantillon d'une couleur visuellement identique si on fait de la peinture. Tout dépend de ce qu'on fera de l'image.
Une fois qu'on aura déterminé une valeur pour ce tronçon, on aura défini notre pixel à l'aide de sa taille et de son contenu.
1.2- Fitrage :
Bien souvent, pour avoir un échantillonnage de bonne qualité, on utilisera différentes méthodes visant à améliorer son rendu final.
Préparation du signal avant échantillonnage :
Pour des raisons d'ordre mathématique (hop, je zappe les détails), il convient généralement de préparer le signal "réel" lors de sa capture pour l'atténuer un peu avant de l'échantillonner. L'idée est que l'infinité des détails du réel pourrait perturber l'échantillonnage, un peu comme si il se perdait dans les détails. Donc on lisse les détails trop fins. Il est possible de faire cette opération de façon électronique (en musique, par exemple, à l'aide d'un égaliseur), ou de façon optique (en altérant la netteté d'une image par exemple).
Maintenant, selon ce qu'on souhaite faire ou les moyens dont on dispose, il est tout à fait possible de ne pas filtrer le signal. C'est d'ailleurs parfois impossible dans certains domaines loins du multimedia. En statistiques, on ne peut pas atténuer l'opinion publique avant de la récolter... on devra donc procéder à des enregistrements suffisamment nombreux pour que l'échantillonnage soit pertinent par rapport à la population testée... mais je m'égare.
Post-traitement :
Il pourra aussi être plus pertinent de traiter le signal après échantillonnage et seuillage (voir ci-dessous) de façon à avoir un traitement plus complexe ou plus adapté. Par exemple, si on veut perdre le moins de qualité possible en évitant un filtrage du signal en entrée, on pourra avoir recours au suréchantillonnage. Sur une image, cela consistera à capturer un multiple des pixels prévus. Par exemple, on pourra capturer 4 valeurs réparties sur un seul pixel, de façon à avoir une image beaucoup plus précise, et ensuite faire la moyenne des 4 valeurs. On aura ainsi une valeur plus précise de ce que contient chaque pixel, sans avoir trop eu besoin de filtrer le signal. C'est ce qu'on appelle le "suréchantillonnage" (mais il existe aussi d'autres cas de figure).
Voici par exemple 2 méthodes de capture d'une image non filtrée. L'une consiste à ne prendre qu'une seule valeur au milieu de chaque pixel. L'autre consiste à faire une "moyenne" de plusieurs valeurs contenues dans le pixel (le suréchantillonnage). Les 2 méthodes donnent un rendu différent sur une même image originale :
 |
|
À gauche, l'image est suréchantillonnée, son rendu est plus "lisse".
À droite, elle ne l'est pas, et le rendu fait apparaître des "crénelages" marqués.
Dans les 2 cas, la taille des pixels représentés est identique.
|
1.3- Le seuillage (ou quantification) :
Cette étape est généralement complémentaire à l'échantillonnage, car la mesure des données enregistrées permet alors de les manipuler plus aisément. C'est une étape indispensable pour que l'image échantillonnée soit traitée et stockée sur un ordinateur.
Elle consiste à mesurer chaque enregistrement. De la même façon que pour l'échantillonnage, on choisira une résolution à cette mesure. Les images sont couramment sauvées en 24 bits par exemple, limitant ainsi la précision des couleurs de façon qu'un enregistrement sera arrondi à la valeur la plus proche. Certains matériels professionnels peuvent travailler avec une meilleure précision.
Ces images numérisées ne prennent toutefois pas encore nécessairement en compte les possibilité techniques d'affichage de l'ordinateur / périphérique. C'est ainsi par exemple que Photoshop peut manipuler des images 64 bits que le PC est bien en mal d'afficher. Aussi, l'Amiga 500 calculait des images qu'il était absolument incapable d'afficher, tout comme on pourrait le faire sur CPC.
1.4- La perte de qualité :
L'image est donc détruite de plusieurs façons :
Pixelisation : L'échantillonnage implique donc une réduction de la précision de l'image par "pixelisation", en résumant une surface de la taille d'un pixel à une simple donnée. Il en résulte une perte de précision par rapport à l'image d'origine, car les éléments la constituant sont réduits à un nombre fini de valeurs : le nombre de pixels (même si la valeur de chaque pixel peut être infinie). En gros, l'échantillonnage transforme l'image en mosaïque. Lorsque la mosaïque est assez grande, alors on peut reconnaître l'image. Si la mosaïque est petite, alors l'image est sérieusement brouillée.
Saturation : On aura une limitation liée à la capacité qu'on a de stocker cette donnée. Par exemple, on peut avoir une saturation des valeurs hautes et basses si la donnée enregistrée dépasse la capacité de stockage (c'est par exemple le cas même en photographie argentique, ou les hautes lumières saturent le film, et où les basses lumières ne le font pas encore réagir).
Bruit : Le signal pourra être perturbé lors de sa réception. Sur un capteur CCD, chaque cellule (pixel) recevant les photons enregistrera une petite différence de tension, liée à sa tolérance propre, dépendant de sa fabrication. Chaque pixel réagira légèrement différemment à une même lumière.
Quantification / seuillage : Lors de la mesure (numérisation de la donnée), on limitera la quantité mesurée à la précision entre 2 graduations. Cette opération qu'on appelle aussi seuillage permet par exemple de choisir une valeur numérique qui pourra ensuite être stockée. Cette valeur est aproximée selon l'échelle de mesure utilisée, de la même façon qu'avec un double-décimètre, on a une perte d'information de l'ordre du millimètre.
|
L'échantillonnage pour les nuls :
Imaginons que nous voulions enregistrer une courbe de la pluviométrie (quantité d'eau tombée) en différents points d'un jardin, pour voir quel est l'effet des zones d'ombre des arbres. On pourra par exemple quadriller le jardin de gobelets en plastiques (ou pluviomètres).
- On aura alors le choix du maillage (qui définit la résolution de l'enregistrement) : doit-on avoir beaucoup de gobelets sérrés tous les mètres, ou seulement tous les 2 ou 3 m ? Dans le premier cas, on aura une mesure très précise des endroits humides. Mais on peut se suffire de la précision des autres cas. C'est ce qu'on appelle l'échantillonnage : on quadrille le jardin de gobelets qui recevront l'eau de pluie à différents endroits, et permettant de mesurer avec une précision choisie la quantité d'eau qu'il tombe en chaque point du jardin. Une première aproximation vient du fait qu'on ne sait pas combien d'eau tombe entre 2 gobelets par exemple.
- L'effet de saturation consiste à découvrir que les gobelets mis sont trop petits, et qu'en cas de forte averse, ils débordent, ne permettant pas dans ce cas d'avoir une mesure de l'eau manquante. On pourrait aussi avoir cet effet pour les précipitation très faibles, où la taille d'un gobelet ne permet pas de récolter la moindre goutte d'eau, car il passe entre 2 gouttes.
- Le bruit, c'est par exemple une feuille qui tombe dans le gobelet, l'erreur de fabrication des gobelets qui leur donnerait une variation de taille ou de porosité, ou l'effet d'évaporation de l'eau une fois récoltée, ou encore une très légère fuite sur un gobelet, ou tout ce qui pourrait altérer la mesure d'un gobelet à l'autre. Le bruit altère la précision de l'enregistrement.
- Enfin, la quantification ou seuillage (ne fait pas partie de l'échantillonnage, mais se révèle nécessaire pour enregistrer les valeurs), est la mesure de la quantité d'eau récoltée dans chaque gobelet, sachant que cette mesure a nécessairement une précision limitée : les graduation d'un verre doseur, de la balance si on pèse l'eau, etc.
Ces gobelets sont à l'image des pixels. Chaque pixel doit être délimité dans un maillage, et c'est l'ensemble des ces pixels qui permet d'avoir une cartographie de l'image.
|
2- Pixels encodés (pour le GPU) :
"Le pixel est l'unité minimale que le contrôleur vidéo peut produire."
D'autres contraintes d'ordre technique s'ajoutent à ces pixels : être affichés une fois qu'ils sont numérisés et traités. Elles sont liées aux possibilités techniques de l'ordinateur qui produira l'image. L'image pourra être traduite par le GPU (Graphical Processing Unit / unité de traitement graphique) qui est un processeur vidéo, mais aussi éventuellement par un programme dirigé vers le port imprimante par exemple. Les contraintes techniques du pixel devront donc se plier aux exigences du périphérique concerné. Par exemple, on n'imaginerait pas réaliser une image en couleurs si elle était destinée à être imprimée en noir et blanc ou affichée sur un écran monochrome, et il serait dommage de ne pas gérer en 3D une image qui serait vue selon un procédé stéréoscopique.
Donc, qu'est-ce qui définit techniquement un pixel ?
Adresse mémoire : Chaque pixel correspond à des informations en mémoire à des endroits précis. Certaines valeurs peuvent très bien se partager entre plusieurs pixels. Par exemple, le choix des couleurs, commun à une zone (sur ZX Spectrum, C64 ou MSX) ou à l'ensemble d'une image (sur CPC). Il existe aussi des cas plus complexes où les pixels peuvent être codés en fonction des pixels précédents (mode HAM sur Amiga par exemple). Sur certaines machines, les pixels ne sont pas complètement indépendants les uns des autres, comme sur Apple 2 par exemple où le décodage se fait par la vidéo. Mais dans tous les cas, des informations sont propres à chaque pixel. Par exemple sur CPC, un octet pourra coder de 2 à 8 pixels selon la résolution. Chaque pixel n'étant modifié que par les bits lui étant associés.
|
Structure de l'octet en mémoire
|
 |
|
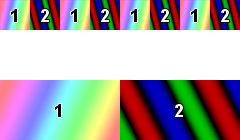
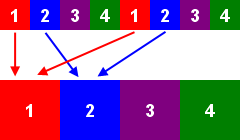
Forme des pixels en mode 0
2 pixels parmi 16 couleurs
|
|
|
|
Structure de l'octet en mémoire
|
 |
|
Forme des pixels en mode 1
4 pixels parmi 4 couleurs
|
|
|
|
Résolution graphique (limitations et décodage des bits) : Chaque ordinateur a sa propre façon de décoder les données en mémoire pour les afficher. Les ordinateurs ont même souvent différentes "résolutions graphiques", correspondant à différentes façons de coder / décoder une image. Ces résolutions graphiques font apparaître essentiellement 2 critères : la finesse d'un point et sa richesse ou profondeur. On ajoutera à cela l'étendue des couleurs affichables.
> profondeur (nombre de bits concernés) : On parle de profondeur pour la "richesse de valeurs" que peut prendre un pixel. Le plus basique étant 1bit=2 valeurs. Dans ce cas, le pixel ne peut avoir que 2 états (éteint / allumé ou couleur 0 / couleur 1 selon les ordinateurs). Lorsque pour un seul pixel, le nombre de valeurs possibles est plus grand, sa "profondeur" augmente. cela permet une plus grande qualité d'image. Par exemple, sur CPC, le mode 2 fait correspondre 1 bit à chaque pixel affiché (2 couleurs au choix), mais en mode 0, il intègre une combinaison de 4 bits pour chaque pixel (donc 16 couleurs différentes possibles).
> nombre de pixels définissant une résolution : sur une surface donnée, plus on a de pixels pour définir l'image, plus le trait sera précis. Sur CPC, on doit choisir entre des pixels fins ou bien des pixels "gros" ayant une plus grande "profondeur" de couleurs. On a en fait le choix d'utiliser 4 bits pour : 4 pixels à 2 états, 2 pixels à 4 états (2 bits chacun), ou 1 seul pixel à 16 états. Sur CPC, les résolutions occupent donc toutes le même espace mémoire. Mais certaines machines utilisent des espaces mémoire de taille différente en fonction de la résolution (Oric, Atari XL, Alice...).
|
160x40 pixels 80x20 pixels 40x10 pixels
|
24 bits
million de couleurs
3 bits
8 couleurs
2 bits
4 couleurs
|
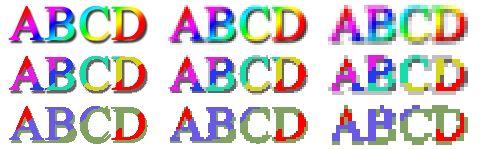 |
|
Différentes résolutions : taille (en pixels) et profondeur (en bits)
|
On peut donc écrire l'équation suivante :
nombre de pixels x profondeur des pixels = poids de l'image (en Ko) = qualité de l'image
Certaines résolutions non standard rendent moins évidente cette équation. Par exemple, l'Amiga disposait d'un mode n'utilisant que 6 bits par pixel et affichant 4096 couleurs en même temps. Le codage un peu spécifique de la résolution permettait des rendus très flatteurs sur des photographies, rendant inexploitable la résolution pour des graphismes de détail. De nombreux 8 bits possèdent une table de couleur, qui est une sorte de masque se superposant aux pixels et définissant des couleurs par zones. Cela permet à des images n'ayant que 2 couleurs par pixel de cumuler 16 couleurs sur une image complète. Certains modèles évolués de MSX disposent de résolutions très avancées utilisant encore cette contrainte en 1990.
 |
Le ZX Spectrum ne peut afficher que 2 couleurs sur des zones de 8x8 pixel (1 bit), ce qui permet en fait d'afficher de nombreuses couleurs sur l'ensemble de l'écran.
Une grille a été ajoutée ici pour visualiser les zones de 8x8.
Cela obligeait parfois les graphiste à user d'astuce pour que l'image ne semble pas limitée par cette contrainte.
|
Comparaison du mode HAM Amiga avec un 6bits classique.
 |
|
Image témoin en 24 bits
L'image d'origine témoin en 24 bits présente des détails et une grande variété de couleurs |
 |
|
Image en 6 bits / 64 couleurs
On garde une grande finesse des contours sur les roses, en revanche, on perd de la précision sur les couleurs. Ces images sont dédiées à la retouche.
|
 |
|
Image en 6 bits / HAM (Amiga)
On perd des détails avec notamment des parasites sur les contours (voir les roses), mais on gagne en dégradés (peau, chevelure). À noter qu'il est très compliqué de retoucher ces images.
|
Définition des couleurs : Il existe différentes façons de définir une table de couleur, selon les ordinateurs. Certains ordinateurs utilisent des valeurs en dur (écrire en rouge par exemple sur MO5), d'autres utilisent des tables d'index (écrire avec la couleur n°1, choisir de mettre la couleur n°1 en rouge, comme sur Amstrad CPC). À noter qu'il existe même des cas où l'ordinateur peut redéfinir sa propre table de couleur (écrire avec l"encre 1, mettre l'encre 1 en rouge, et redéfinir les paramètres de "rouge" en le transformant en bleu, comme c'est le cas sur le KC Compact).
La définition d'une couleur intègre des paramètres d'affichage différents d'un ordinateur à l'autre. Dans certains cas, on aura du YUV (AtariXL, Plus4), dans d'autres du RVB (CPC, Atari ST), ou simplement une luminance (ZX81). Certaines résolutions du MSX intègrent même une définition TSL (teinte, saturation, luminosité).
3- Pixels affichés (par un périphérique) :
C'est le plus petit point que le périphérique peut produire.
Par exemple, l'écran, une imprimante ou traceur, un projecteur, etc. Ce périphérique comprendra un signal numérique en entrée qu'il interprétera en image avec ses propres contraintes. Un pixel n'aura donc pas le même rendu en fonction du périphérique. La taille et la qualité d'un écran par exemple pourront changer ses propriétés.
Qu'est-ce qui définit ce pixel sur ce périphérique ?
- Position : Elle se détermine de façon absolue par rapport à la surface d'affichage, mais la position relative d'une couleur par rapport à une autre peut aussi avoir une incidence. C'est précisément cet aspect qui peut être intéressant à gérer pour un bon traitement du détail.
- Forme : D'un écran à l'autre, le pixel pourra avoir un ratio x/y différent. Par exemple, l'écran monochrome du CPC est différent de l'écran couleur, et les pixels n'ont pas la même forme sur ces 2 écrans vendus par Amstrad. Les écrans LCD ont des rectangles très saillants, tandis que les CRT ont des pixels presque ronds.
- Taille : Cela dépend essentiellement de la taille de l'écran. Mais cela peut aussi dépendre d'un choix à l'impression, selon une homothétie. La qualité dépend ainsi de la taille de l'affichage. Plus une même image est affichée petit, plus la qualité est grande et inversement. C'est le rapport pixel / dpi que les graphistes ont souvent du mal à appréhender (croyez-en ma lonnngue expérience).
- Flou : Les écrans LCD sont particulièrement nets par rapport aux écrans CRT ou aux écrans à plasma. Le rendu y est donc très différent. Par contre, les écrans LCD ont un décalage de couleurs en X que n'ont pas réellement les écrans CRT. On ne parlera pas de flou sur une impression papier, mais plutôt de "précision de point".
- Stabilité : Les moniteurs CPC, comme les télévisions affichent une image à une fréquence de 50Hz (60Hz dans d'autres pays). Cette fréquence passe généralement à 75 ou 85 Hz pour les écrans cathodiques sur PC. Le scintillement des LCD est de l'ordre de 20 000 Hz (celle du rétro éclairage). Le rendu d'une image est différent dans tous ces cas de figure. Lorsqu'une image est affichée en "flipping", sa résolution de 25Hz change encore bien des choses sur le confort de l'image.
- Grain : Il dépend de nombreux paramètres, et tout le monde n'utilise pas nécessairement la même définition à ce terme. Personnellement, je parle du grain de l'image, lié au medium (l'écran). Par exemple, le rendu est différent sur une télévision (photophores alignés verticalement) ou sur un écran de PC (photophores à disposition hexagonale), ou encore selon la qualité du papier pour une impression, de l'encre, ou du mode d'impression (on ne parle plus de pixel en impression offset que chez les anglophones).
|
|
|
Les photophores de différents écrans peuvent donner une rendu différent à l'image.
À gauche un moniteur CPC, à droite, un moniteur PC. (photo : Cloudstrife)
|
- Couleurs : Elles peuvent dépendre de la technologie de l'écran (gamma très important sur les CRT et presque plat sur les LCD) ou de ses réglages d'usine. Aussi, il est rare de trouver 2 écrans LCD ayant le même rendu de couleur. Cela dépendra aussi du mélange utilisé, par exemple en impression où la synthèse des couleurs se fera avec 3, 4, 7 encres ou +, choix de tons directs... Par exemple, la console Vectrex avait un écran affichant des couleurs par tons directs sur les layers qui masquaient l'image dessinée à l'aide d'un faisceau blanc. Ce cas reste cependant unique en son genre.
- Agencement : On a généralement un agencement de pixels orthogonal, mais il existe des cas où leur agencement est hexagonal. C'est le cas sur les écrans d'appareils photo numériques par exemple. Mais il est possible de reproduire cet agencement sur certains ordinateurs comme le C64, en décalant chaque ligne d'un demi-pixel en X.
 |
L'écran LCD de nombreux appareils photo numériques ou camescopes ont des composantes RVB décalées d'une ligne à l'autre de façon à améliorer le rendu des photos.
Par contre, cela détériore le rendu des textes...
(photo : Boz)
|
- Etc.
|

